What I refer to as the p+1 problem is this conjecture:
Conjecture: Every rational z can be represented in the form z=(p+1)/(q+1) with p and q being prime integers.
I have verified this conjecture for integers to 109. Some calculations and conjectures related to this computation are at the Journal of Integer Sequences, Vol. 4.
I have also verified this conjecture for all rationals z with 0 ≤ z ≤ 1 with denominator not more than 1000.
Let f(a,b) = the minimal positive integer m such that am-1 and bm-1 are both prime. Then the conjecture implies that f(a,b) is well-defined for all rationals a/b in simplest form.
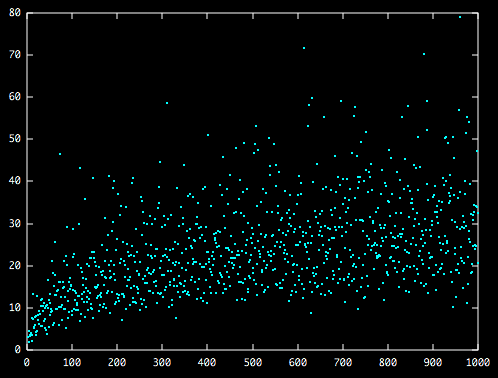
Here is a plot of f(a,b) for 1 ≤ b &le 1000, 1 ≤ a ≤ b, with (a,b)=1. The horizontal axis is b and the vertical is f(a,b) (so there are multiple points for each b). The cyan points are f(a,b) while the yellow points are the mean values of f(a,b) for each b.

Next is a plot of just the averages. We can see there is a general increasing trend. I expect f(a,b) = O(log2 b), at least on average, but, of course, it has not been proved that f(a,b) is even finite.
Since bm-1 is more likely to be prime if b has a lot of small prime factors, we would expect that f(a,b) would be smaller, on average, for those b with lots of small prime factors. Here is a plot of the average values of f(a,b) (as in the plot above) versus sigma(b)/b, a measure of the "abundance" of b. It does seem to indicate that large values of sigma(b)/b tends to keep f(a,b) small.

back to mathematics